Estimation du risque

L’estimation du risque consiste à fournir des mesures explicites de la survenue d’un danger et de l’incertitude associée. En santé des plantes, l’estimation du risque varie généralement dans l’espace et le temps, du fait des facteurs de risque spatialement ou temporellement hétérogènes (e.g., occupation du sol, variables climatiques, transports) et de la dynamique du pathogène, ravageur ou contaminant considéré. 

Décomposition du risque 

► Description

Le risque lié à un organisme nuisible peut être estimé à travers l’espace géographique via une décomposition simple résumée par l’équation suivante : 

W_i = P_i x R_0i

où W_i est le risque estimé au site géographique i, P_i est la probabilité que l’organisme nuisible arrive dans le site i, et R_0i est la taille de l’épidémie attendue localement dans le site i. Cette décomposition a été utilisée par Parnell et al. (2014) afin de construire une stratégie de surveillance, dite basée sur le risque, d’un organisme nuisible dans un contexte épidémique. Selon le contexte (e.g., épidémie, endémie, territoire indemne), diverses modélisation des termes P_i et R_0i peuvent être proposées.

► Exemple d'application

L’approche de Parnell et al. (2014) a été appliquée pour cartographier le risque lié au nématode du pin, dans le contexte d’un territoire indemne, en l’occurrence la France métropolitaine. Cette cartographie du risque est vue comme une étape préliminaire pour construire in fine une stratégie spatialisée de surveillance du territoire fondée sur le risque. L’application de l’approche de Parnell et al. (2014) nécessite la partition de la France en un certain nombre de sites appelées également unités épidémiologiques (e.g. les départements ou des quadrats de surfaces constantes). La probabilité P_i que le nématode du pin arrive dans le site i a été modélisée comme une fonction, notamment, des flux de marchandises contenant du bois de pins qui arrivent et transitent par la France, et des stocks de produits bois issus de pins (palettes, caisses, ...) dans les entreprises, les scieries et les pépinières. La taille R_0i de l’épidémie  attendue localement dans le site i a été modélisée comme une fonction dépendant de la surface d’hôtes sensibles au nématode du pin dans le site i, d’une estimation du nombre de vecteurs présents dans le site i et du dépassement du seuil de 20°C par la température moyenne en juillet (Rutherford et al. 1990). Le produit de ces deux quantités est une estimation du risque W_i d’émergence (introduction + établissement) du nématode du pin dans le site i.

► Notes et références

Parnell, S. et al. (2014). A generic risk-based surveying method for invading plant pathogens. Ecological Applications, 24 (4), pp. 779-790.

Rutherford, T.A. et al. (1990). Nematode-Induced Pine Wilt Disease: Factors Influencing Its Occurrence and Distribution. Forest Science, 36 (1), pp. 145-155.

PROMETHEE | Aide à la décision multicritère

► Description

PROMETHEE (Preference Ranking Organization METHode for Enrichment Evaluations) est un algorithme de hiérarchisation et d’aide à la décision fondé sur des critères multiples et des fonctions de préférences associées. La hiérarchisation fournie par PROMETHEE est matérialisée par un score prenant une valeur numérique entre -1 et 1, qui peut être ramenée entre 0 et 1 pour l’interpréter comme une probabilité liée au risque. 

► Exemple d'application

L’algorithme PROMETHEE a été utilisé dans le cadre de l’estimation du risque d’entrée du nématode du pin en France. Onze critères ont été utilisés pour déterminer ce risque, parmi lesquels : (1) des données de transports de marchandises par différentes voies de communication (ferroviaire, aérienne, maritime, routière), (2) des données d’approvisionnement en bois de conifères dans les scieries françaises, (3) des données de densité de populations hôtes, (4) des données sur l’origine de l’importation des palettes, (5) des données relatives aux sites où sont opérées sciages, grumes ou caisses et aux sites de transformation de bois de conifères. Un poids a été associé à chacun de ces critères, en s’appuyant sur des dires d’experts. Cette méthode a permis de classer les zones d’étude (en l’occurrence les départements français) en fonction de l’importance du risque d’entrée du nématode du pin selon les 11 critères.

► Notes et références

http://www.promethee-gaia.net/FR/

Apprentissage automatique

► Description

Les méthodes d’apprentissage automatique (ou machine learning) sont des algorithmes capables, de manière générique, d’apprendre à prédire un phénomène à partir de données relatives audit phénomène. En général, ces méthodes sont implémentées (i) en entraînant l’algorithme à faire de la régression ou de la classification sur un jeu de données d’entraînement (ce qui permet de calibrer les différents paramètres du modèle de régression ou de classification) et (ii) en soumettant à l’algorithme un nouveau jeu de données sur lequel il doit accomplir la tâche de régression ou de classification pour laquelle il a été conçu. L'apprentissage est dit “supervisé” lorsque la réponse à la tâche de régression ou de classification est connue dans le jeu de données d’entraînement. Il est dit “par renforcement” lorsque le modèle est calibré de manière incrémentale en fonction des récompenses reçues par l’algorithme lorsqu’il remplit sa tâche de manière plus ou moins efficace. Il est dit non supervisé lorsqu’il doit apprendre, par exemple, à classifier sans connaissance de la classification réelle dans le jeu de données d’entraînement. 

Parmi les algorithmes d’apprentissage, on compte les arbres de décision (forêts aléatoires, boosting), les réseaux de neurones ou encore les méthodes basées sur les ‘k plus proches voisins’. Plusieurs packages du logiciel R permettent d’appliquer ces algorithmes, par exemple randomforest, xgboost, rpart (spécifiques à une méthode) ou encore mlr et caret (qui regroupent au sein même du package un grand nombre d’algorithmes d’apprentissage).

► Exemple d'application

Dans le cadre de la surveillance de la bactérie Xylella fastidiosa, une des missions de l’équipe opérationnelle de la Plateforme ESV est de réaliser des cartes de risque afin d’identifier les zones les plus à risque concernant la présence de la bactérie. Pour ce faire, le territoire français a été partitionné en unités épidémiologiques (ici des quadrats de 2km²), dans lesquelles ont été récupérées des informations telles que la présence ou l'absence de la bactérie, l’occupation du sol et des variables climatiques. Ces données ont ensuite été utilisées, dans un cadre d’apprentissage supervisé, pour prédire la présence de la bactérie dans des zones non échantillonnées par exemple et pour évaluer les zones indemnes les plus à risque. 

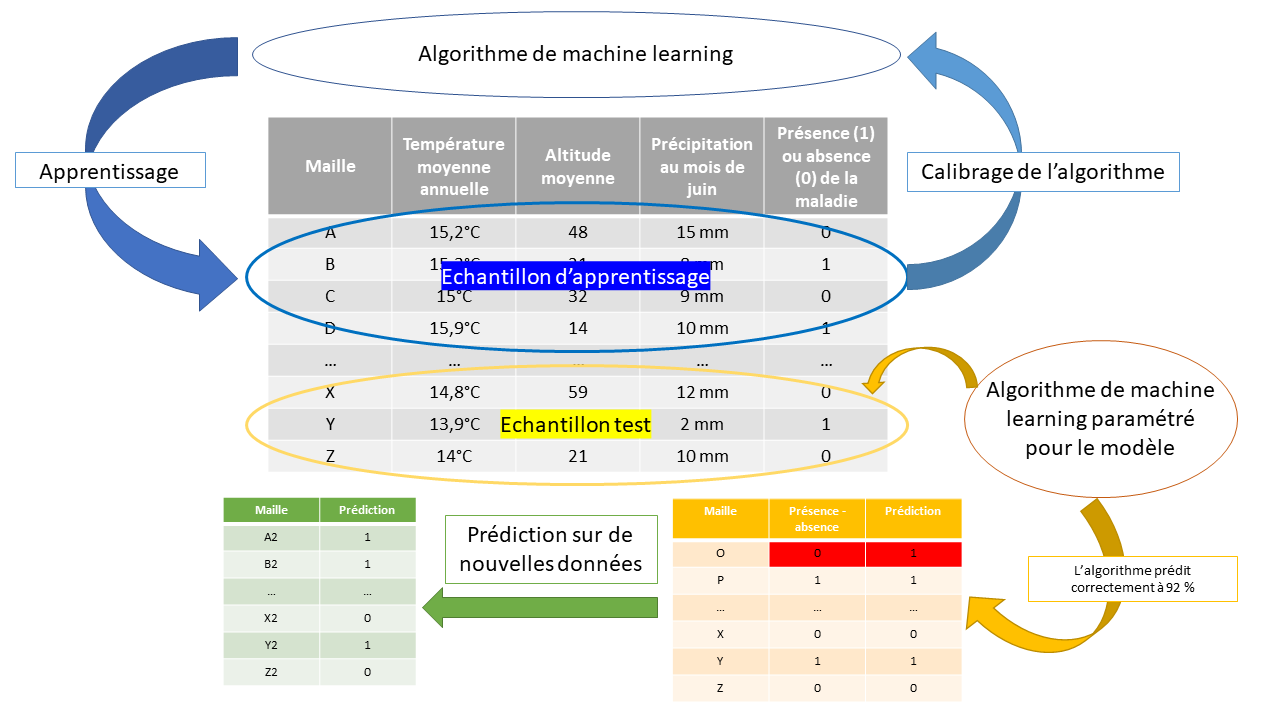
Le schéma ci-dessous illustre le chemin suivi par un algorithme d’apprentissage entre les données et les prédictions. 

• L’échantillon de données d’apprentissage sert à calibrer l’algorithme (cela représente environ un tiers des données totales disponibles dans ce jeu de données). 
• L’échantillon test permet de vérifier et valider les prédictions issues de l’algorithme une fois celui-ci calibré. (environ les deux autres tiers des données).
• L’algorithme réalise des prédictions sur de nouvelles données. 

► Notes et références

Bischl, B. et al. (2020). mlr: Machine Learning in R. R Package. 

Kuhn, M. et al. (2020). caret: Classification and Regression Training. R package.

Breiman, L. et al. (2018). randomForest: Breiman and Cutler's Random Forests for Classification and Regression. R package.

Chen, T. et al. (2019). xgboost: Extreme Gradient Boosting. R package.

Therneau, T. et al. (2019). rpart: Recursive Partitionnning and Regression Trees. R package. 

Martinetti, D. & Soubeyrand, S. (2018). Identifying Lookouts for Epidemio-Surveillance: Application to the Emergence of Xylella fastidiosa in France. Phytopathology. 109.

Calculs de distances

► Description

Une distance mathématique fait référence à une notion de distance/longueur entre deux points dans un espace à plusieurs dimensions. Plus la distance sera proche de 0 plus les deux points seront similaires et/ou proches dans l’espace. Il existe différentes distances : euclidienne (distance à vol d’oiseau), de Manhattan (déplacement sur un réseau : un taxi sur un réseau routier par exemple), de Tchebychev (différence maximale entre les coordonnées de deux points sur une dimension), de Levenshtein (distance entre deux chaînes de caractères). Les distances, qu'elles soient géographiques ou dans des espaces de variables explicatives par exemple, constituent des outils présents dans nombre d’analyses statistiques visant à estimer des risques. 

► Exemple d'application

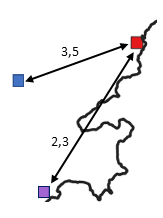
Sur l’illustration présentée ci-dessous, supposons que le site rouge soit infecté par la bactérie Xylella fastidiosa et que la bactérie n’ait pas été détectée dans les sites bleu et violet. Pour évaluer le site observé indemne le plus à risque, on peut calculer la distance géographique entre les sites, le site le plus proche (le bleu) étant celui le plus à risque. On peut également calculer la distance euclidienne entre les environnements des deux sites observés indemnes d’une part et du site infecté d’autre part, par exemple avec la fonction dist du logiciel R. Au vu des valeurs de cette distance données sur le schéma, le site violet présente un environnement plus similaire à celui du site rouge que le site bleu et est donc plus à risque. Un des enjeux des méthodes d’apprentissage est de “pondérer” la proximité géographique et la proximité environnementale pour in fine estimer le risque de manière efficace en prenant en compte divers critères.

► Notes et références

Wong, J. (2013). pdist : Partitioned Distance Function. R package. 

MESS | Mesure de similarité environnementale

► Description

L’algorithme MESS a été développé par Elith J. et al. (2010) et a pour objectif de calculer comment un point est similaire à un référentiel de points. Cet algorithme se base sur un ensemble de variables prédictives. Il attribut une valeur négative pour les variables d'un point se trouvant en dehors des valeurs des variables de points référentiels. 

► Exemple d'application

L’algorithme MESS est utilisé dans le cadre de l’élaboration de la carte de risque de Xylella fastidiosa en France métropolitaine. L’algorithme parcourt l’ensemble des mailles qui quadrillent la France et les compare une à une à l’ensemble de mailles où la bactérie a été détectée en France. Les valeurs de l’algorithme permettent d’identifier des mailles présentant un environnement similaire aux mailles des zones infectées.

► Notes et références

Elith, J. et al. (2010). The art of modelling range-shifting species. Methods in Ecology and Evolution, 1, 330-342.

Marjou, M. et al. (2019). Risk-based surveillance strategies for early detection of Xylella fastidiosa in continental France. Poster. 2ème conférence sur Xylella fastidiosa. Ajaccio, octobre 2019.

Noyaux de dispersion

► Description

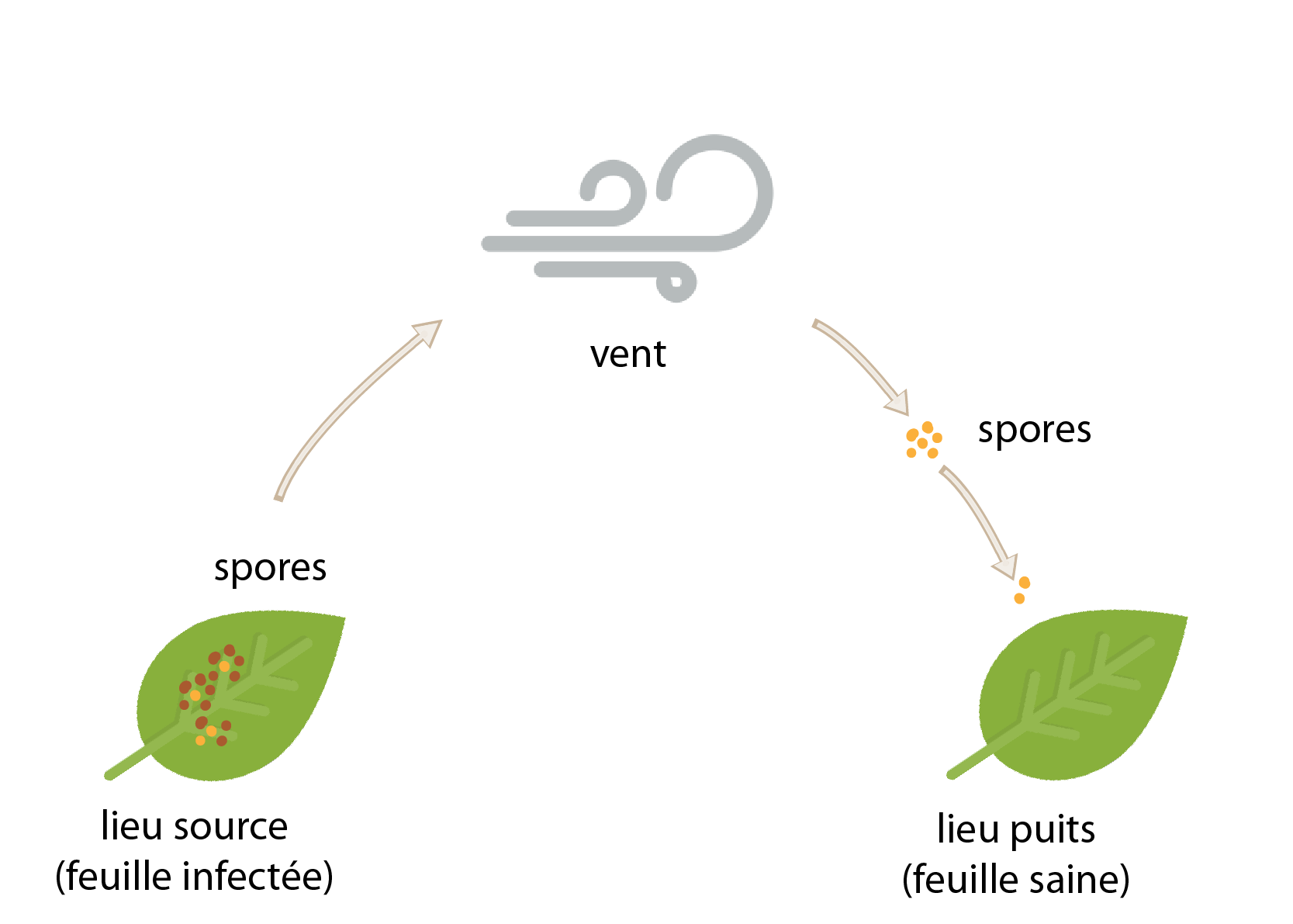
Un noyau de dispersion est une fonction mathématique modélisant la répartition spatiale attendue des positions de dépôt d’agents de dissémination émis depuis un lieu source donné. Cette fonction mathématique tient compte dans sa forme et ses paramètres des caractéristiques fondamentales du processus de dispersion des agents de dissémination en question (i.e. dispersion par le vent, l’eau, l’humain ou les animaux). Le noyau de dispersion peut également être exprimé en terme de répartition des distances de dispersion plutôt que des positions de dépôt.

► Exemple d'application

Un noyau de dispersion Gaussien (favorisant les dispersion à courte distance) est utilisé pour modéliser les probabilités de dispersion du nématode du pin dans le cas d’une possible émergence d’un foyer en France. Ce noyau de dispersion est fonction des distances de vol naturel de son vecteur, Monochamus galloprovincialis. 

► Notes et références

Nathan, R. et al. (2012). Dispersal kernels: review. Chapter 15. Dispersal Ecology and Evolution.